4. 선로 정수와 코로나
4.3 인덕턴스
4.3.2 직선상 도선의 자속
직선상 도선의 자속
먼저 도체 외부에 대해서 그림 4.3처럼 반지름 r [m]의 도선의 중심 O로부터 x [m]의 거리에 dx [m]의 두께로 도선에 따라서 길이 1 [m]의 원통상의 자기 회로도를 생각해 보자.

이 도체에 전류 I가 흐르고 있을 경우 도체 중심으로부터 x만큼 떨어져 있는 곳에서의 자계의 세기 Hout은 암페어의 주회 법칙으로부터

이고, 이때 자속 밀도 Bout은


그러므로, 그림의 도선 외부 단면의 미소 부분을 통과하는 자속 dΦ는

가 되고, 도선의 권선 회수는 1이므로 dx 부분에 의한 쇄교 자속수 dφ는 다음과 같다.
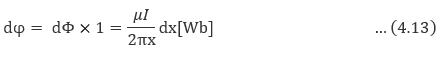
그러므로 도체 표면인 반지름 r [m]부터 S [m]만큼 떨어져 있는 범위 내의 쇄교 자속수 φout은 위 식을 x=r에서부터 x=S까지 x에 대해서 적분한 값이 된다.

다음에 도체 내부를 생각한다. 도체 내부의 자속 쇄교수를 구할 경우에는 우선 기본적인 가정으로서 도체에 흐르고 있는 전류 i [A]는 반지름 r [m]의 단면을 균일하게 분포되고 있는 것으로 한다.

지금 그림 4.3(c)처럼 도체의 중심 O로부터 반지름 x [m]의 원을 그리고 외부 자속 쇄교 자속수를 구했을 때와 마찬가지로 반지름 (x+dx)[m]의 원을 그린다.(곧 이것이 두께 dx [m]로 길이 l [m]인 동심 원통이 된다.)
반지름 r [m]의 원의 단면적 πr² [㎡]이고 반지름 x [m]의 단면적은 πx² [㎡]이다. 앞서 전류 i는 단면에 균일하게 분포해서 흐르고 있다고 가정하였으므로 반지름 r [m]의 단면에 흐르고 있는 전류 i [A]와 반지름 x [m]의 면적에 흐르고 있는 전류 ix [A]와는 면적에 비례한 크기가 되므로

로부터 다음식을 얻는다.

이 전류가 도체의 중심에 집중되어 있다고 하면, 두께 dx [m], 길이 d [m]인 원통의 단면을 통과하는 자속 식 (4.12)로부터

가 되고, 이 자속은 반지름 x [m]인 원통 내부의 도체 부분만을 쇄교 한다. 따라서 전류 Ix와 자속과의 쇄교수 dφ는 다음과 같다.

그러므로 도체 내부의 단위 길이당 쇄교 자속수 φin은 식 (4.17)을 x=0에서부터 x=r까지 x에 대해서 적분한 값이 된다.

이 결과 도선의 내·외부의 단위 길이당의 총 자속 쇄교수는 다음과 같다.

이 식은 다음과 같이 간단하게 할 수 있다.

즉, 전 쇄교자속수는 새로운 반지름 r'[m]인 도체 외부의 쇄교 자속수와 같으며, 이때 r'을 도체의 등가 반지름 또는 기하 평균 반지름이라고 한다.
'송배전공학_공부' 카테고리의 다른 글
| 27. 선로정수(인덕턴스) - 대지를 귀로하는 인덕턴스 (1) | 2023.01.17 |
|---|---|
| 26. 선로정수 (인덕턴스) - 도선의 인덕턴스 일반식 (0) | 2023.01.14 |
| 24. 선로정수 (인덕턴스) (0) | 2023.01.13 |
| 23. 선로정수 (저항) + 표피효과 (1) | 2023.01.12 |
| 22. 선로정수의 개요 (0) | 2023.01.12 |



